1931 ⟶ Gödel Proves Limits of Algorithmic Theorem Proving
Kurt Gödel encoded mathematical statements and proofs as int...
Year
1763
1854
1931
1935
1937
1971
📊 Bayes' Theorem Laid the Groundwork for Bayesian Networks
Thomas Bayes's work An Essay Towards Solving a Problem in the Doctrine of Chances, published two years after his death, laid the foundations of Bayes' theorem and used in modern AI in Bayesian networks.⟶
ProbabilityStatisticsBayesian inferenceBayesian networksMathematicsMachine LearningAlgorithmsFoundations
United Kingdom➕ Boole Invents Boolean Algebra
George Boole set out to "investigate the fundamental laws of those operations of the mind by which reasoning is performed, to give expression to them in the symbolic language of a calculus", inventing Boolean algebra.⟶
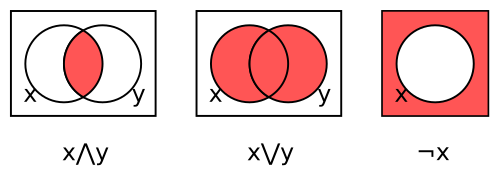
Boolean algebraLogicMathematicsSymbolic logicComputationFoundationsComputer scienceReasoning
United Kingdom♾️ Gödel Proves Limits of Algorithmic Theorem Proving
Kurt Gödel encoded mathematical statements and proofs as integers, and showed that there are true theorems that are unprovable by any consistent theorem-proving machine. Thus "he identified fundamental limits of algorithmic theorem proving, computing, and any type of computation-based AI," laying foundations of Theoretical computer science and AI theory.⟶
Gödel's incompleteness theoremsMathematicsLogicComputabilityTheorem provingLimits of computationTheoretical computer scienceFoundations
Austriaλ Church Proves the Undecidability of the Decision Problem and Develops Lambda Calculus
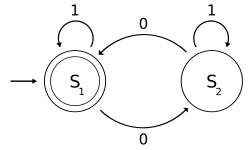
Alonzo Church extended Gödel's proof and showed that the Decision problem of computer science does not have a general solution. He developed the Lambda calculus, which will eventually be fundamental to the theory of computer languages.⟶
UndecidabilityDecision problemLambda calculusComputabilityTheoretical computer scienceProgramming languagesAlgorithmsChurch-Turing thesis
USA💻 Turing Introduces the Turing Machine and Proves the Halting Problem Undecidable
Alan Turing published "On Computable Numbers", which laid the foundations of the modern Theory of computation by introducing the Turing machine, a physical interpretation of "computability". He used it to confirm Gödel by proving that the Halting problem is undecidable.⟶
Turing machineHalting problemComputabilityTheoretical computer scienceAlgorithmsFoundationsAlan TuringComputation
United Kingdom